앞서배운 팩토리얼 코드에서 재귀함수에 대해서 알아보았는데요
자기 자신을 호출하는 재귀 호출은 피보나치 수열의 알고리즘에서도 사용됩니다.
피보나치 수열은
앞의 두항을 합친 값이 다음 항이 되는 수열 입니다.
처음에 1부터 시작한다고 하면
1, 1, 2, 3, 5, 8, 13, 21.... 이런식으로 나타낼 수 있습니다.
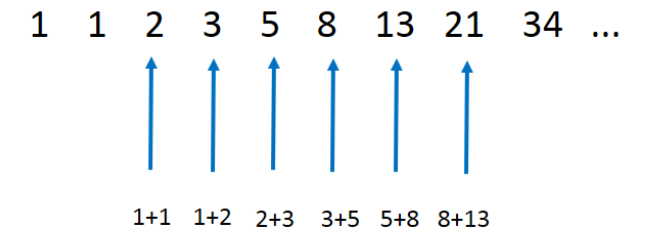
한 7, 8번째 항까지는 손으로도 쉽게 구할 수 있을텐데
피보나치수열의 30번째 항을 구하라고 한다면 ?
손으로는 약간 무리가 올거같고 그렇다고 못할것도 없어서 노가다를 뛰어서 구했는데
계산 실수라도 해서 잘못구하면
마음이 많이 쓰라릴거같습니다.
그래서 피보나치수열을 일반항 공식을 사용해서 구하자니 이거
우리가 중,고등학교때 배운 그런 쉬운 공식이 아닌데요
피보나치 수열의 일반항은

입니다.
여기에 30을 때려 넣고 계산하자니 그것도 쉽지가 않네요...?
아니 그냥 손으로 덧셈하는게 더 빠를 것 같습니다.
30제곱승을 계산하는거 자체가 말이 안되기 때문이죠 😂😂😂😂😂😂
그래서 사람들이 계산기를 발명하고
그러다 또 안되니까 컴퓨터가 나온거 아닐까요?
우리가 손으로 안되면 컴퓨터한테 명령만 내리면그만인것을
그래서
오늘은 피보나치 수열의 N번째 항을 구하기 위한 코드를 알아보도록 하겠습니다.
피보나치 수열의 함수에서 n번째 항은
n-2 번째 항과 n-1번째 항의 합 입니다.
예시로 피보나치 수열의 6번째 항은
수열의 5번째 항과 4번째 항의 합이며
5번째 항은 4번째 항과 3번째 항의 합,
4번째 항은 3번재 항과 2번쨰 항의 합
3번째 항은 2번째 항과 1번째 항의 합
.
.
입니다.
여기서 눈치가 빠르신 분들이나 , 팩토리얼 재귀함수 코딩 글을 읽어 보셨다면
피보나치 함수 안에 피보나치 함수가 존재한다는걸 알 수 있을것 같습니다.

이는 재귀적인 호출이며 오늘은 이 표현을 사용하여
피보나치 수열을 알고리즘을 코드로 구현해보겠습니다.
자바로 구현 하였으며,
다른 언어도 문법은 다르겠지만 방식을 똑같습니다.
재귀호출을 사용하여 피보나치수열 코드 만들기
public static int fibonacci(int n) { // 수가 길어질때는 long형 사용
int one = 1; // 피보나치 수열의 첫번째 항
int two = 1; // 피보나치 수열의 두번쨰 항
if (n == one) { // 구하고자 하는 항이 첫번째 항일경우
return one; // 첫번째 항을 반환 합니다.
}
else if (n == 2) { // 두번째 항일 경우
return two; // 두번째 항을 반환 합니다.
}
else {
return fibonacci(n-1) + fibonacci(n-2); // n번째 항을 구하기 위해 n-1번째 항과, n-2번째 항을 다시 불러와
더한 뒤 반환 합니다. 여기에서 재귀호출을 사용합니다.
}
}
이렇게 되면 피보나치 수열의 n번째 항을 구할 수 있게 됩니다.
그럼 이 함수를 사용해 아까 구하려고 했던 피보나치의 30번째 항을 구해보도록 하겠습니다.

그냥 숫자만 툭 내뱉으면 정이 없어보이니까
몇가지 멘트만 추가해서 만들어 봤습니다.
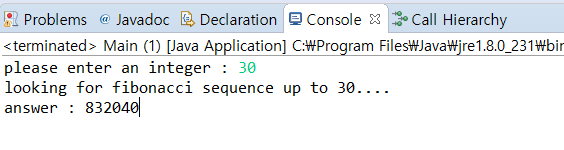
제대로 작동하는걸 확인 할 수 있습니다.
우리가 구하고 했던 피보나치 수열의 30번째 항은
832040 이었네요
그런데 피보나치수열은 이렇게 숫자 하나만 뱉으면 정이 없어보이니까
n번째 항 전까지들도 추가 해주겠습니다.

n번째 항을 구하면 n번째 항까지의 수열을 전부 나타 내도록 수정하였습니다.
다시 30번째 항을 구하면

1항부터 30항까지 나타내어지는걸 볼 수 있게 됩니다.
재귀적인 표현에 대한 이해를 하였고 코드로도 만들었으며 계산도 하면 이제는
피보나치 수열의 100번째 항도 구할 수 있겠죠?
저 코드를 사용해서 구해보시면 될거같은데...
아마아마아마 무지 오래 걸리실 겁니다.
몇시간도 더 걸리실지도 몰라요
기억만 하고 있으면 참 편리할텐데
다음 글에서는 재귀호출의 중복계산 스택의 팝업을 피하고
피보나치 수열의 100번째 항을 구해보도록 하겠습니다.
도움이 되셨으면 좋겠습니다. 땡큐
'JAVA' 카테고리의 다른 글
| 자바상식 (0) | 2023.12.21 |
|---|---|
| 자바로 만든 스윙 기반의 GUI 프로그램 (1) | 2020.09.13 |
| 프로그래머스 자바 전화번호 목록 (0) | 2020.09.10 |
| 팩토리얼 함수 코딩, 알고리즘 ,Factorial Algorithm (재귀함수) (0) | 2020.02.24 |
| 팩토리얼 함수 코딩, 알고리즘 , Factorial Algorithm (반복함수) (5) | 2020.02.24 |



댓글